练习由各种 Sorting algorithm 实现的网络相关编程。
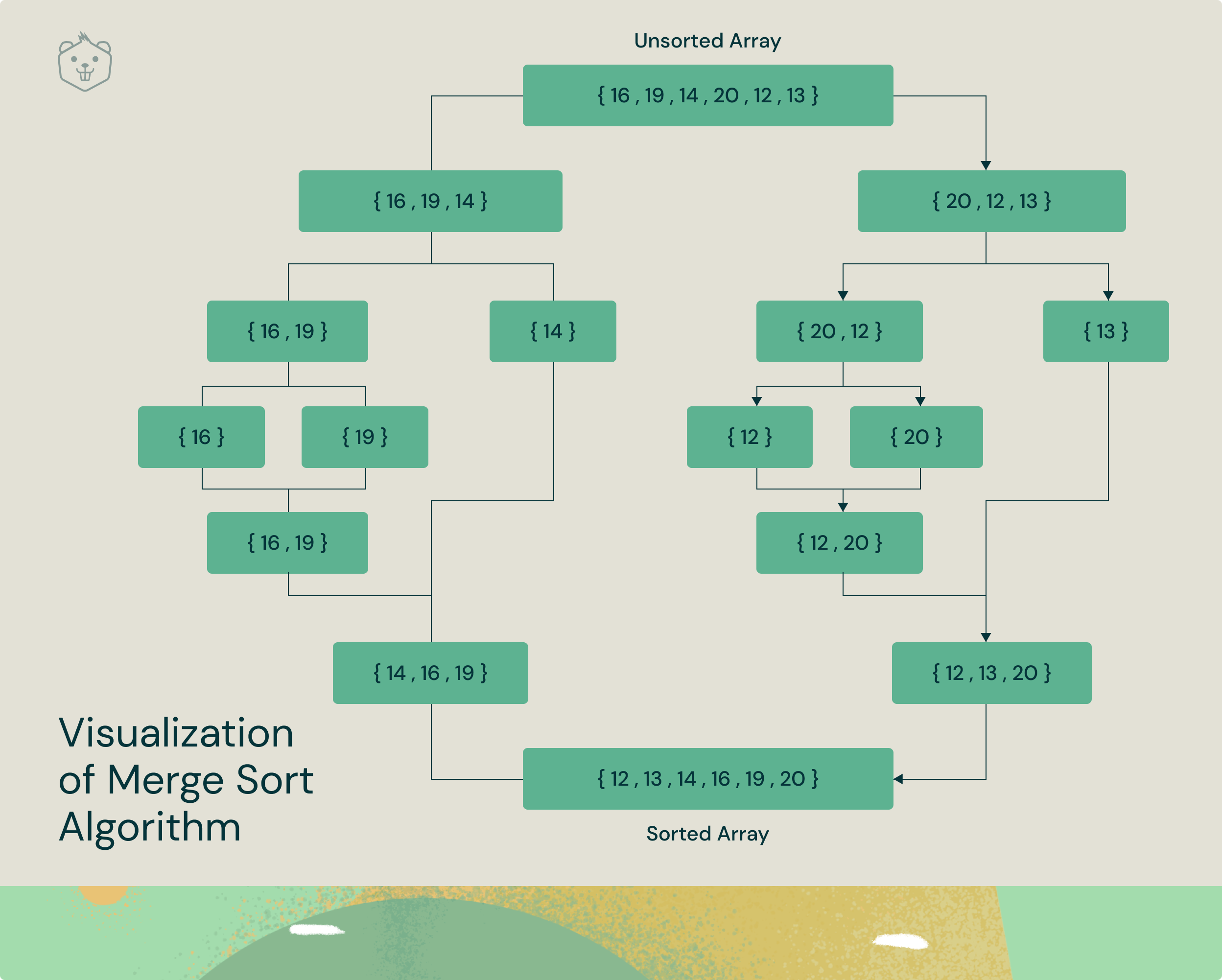
Goals
- Understanding the sorting algorithms presented in class in further depth.
- Introduction to fixed soting networks.
- Compare code speed by comparing length.
Task 1: Fixed Bubble Sort
Introduction
A “sorting network” is a bunch of “compare and exchange” (also known as
compare and swap) operations that are fixed and arranged in a particular
sequence to sort a list of a particular length. These networks do not use any
loops or recursion.
For example, a compare and exchange operation in python might look like:
if a_list[3] > a_list[4]:
a_list[3], a_list[4] = a_list[4], a_list[3]
—|—
or
if a_list[3] > a_list[4]:
temp = a_list[4]
a_list[4] = a_list[3]
a_list[3] = temp
—|—
Both of the above pieces of code do the same thing. The first method of
swapping is available in Python, but doesn’t exist in many other programming
languages.
To sort a list that’s always length 2, we can just use the following code:
def bubble2(a_list):
if a_list[0] > a_list[1]:
a_list[0], a_list[1] = a_list[1], a_list[0]
return a_list
—|—
For sorting a list of length 2, we need exactly one compare/swap.
For sorting a list of length 3, using bubble sort, bubble sort in the first
outer loop compares exchange index 0 with index 1, then index 1 with index 2.
If the item at index 0 is the largest item, it will “bubble up” to index 2
during this iteration. That is, you need to use the bubble sort that iterates
like this:
for bubble in range(0, n):
for index in range(0, n - bubble - 1):
—|—
Then in the second iteration of the outer loop, it compares and exchanges
index 0 with index 1.
This is the second bubble, but it doesn’t need to go all the way to the end,
since the end is gauranteed to already have the largest item. So we can always
sort a list of length 3 with the following code:
def bubble3(a_list):
# bubble 0
if a_list[0] > a_list[1]:
a_list[0], a_list[1] = a_list[1], a_list[0]
if a_list[1] > a_list[2]:
a_list[1], a_list[2] = a_list[2], a_list[1]
# bubble 1
if a_list[0] > a_list[1]:
a_list[0], a_list[1] = a_list[1], a_list[0]
return a_list
—|—
Implementing Fixed Bubble Sort
Your goal for task 1 is to use the functions you made in task 1 to create a
function fixed_bubble(size) which takes one argument. That argument will
determine the length of the list that can be sorted. fixed_bubble(size) should
output a file that contains a function that uses bubble sort to sort lists of
length size. For examples, fixed_bubble(2) should create a bubble2.py that
contains the above bubble2 function that takes a single argument (a list) to
be sorted. Similarly, fixed_bubble(3) should create a bubble3.py that contains
the bubble3 code above (or simlar code).
Your output code doesn’t have to be exactly like the above code, it can
contain comments, you can use a different swap, etc. It doesn’t matter whether
you use a_list[0] > a_list[1] or if you use a_list[1] < a_list[0] ,
etc. It should just consist of a function with a big sequence of compare and
exchange, however you want to write them and a return at the end. You can add
comments or not. Adding comments in the output program can be helpful for
debugging.
However your output sorting programs must not contain any loops, recursion,
imports, or anything that gets Python to do loops or recurison or sorting for
you. That means no for, while, map, etc. And definitely no sort or sorted or
anything that sorts. Several of these keywords are checked by check1.py so be
sure to avoid using names like list, or check1.py will fail. (Using a name
like a_list or some_list is fine.) As always, check1.py can’t check for every
way to do a loop or recursion in Python, but you still can’t have any in your
code, regardless of what check1.py says.
Loops, for, while, sort, sorted, and recursion are 100% okay to put in your
a3.py, but should never appear in the generated output programs like
bubble4.py.
Additional example outputs are available in the files below: bubble4.py, etc.
Task 2: Bitonic Sort
Bitonic sort is a sorting routine that like Mergesort involves recursively
splitting and merging. Unlike mergesort, it doesn’t require any extra space.
Mergesort requires copying back and forth between at least two lists. Bitonic
sort sorts everything while leaving it in the same list, like bubble sort
does. So, it kind of combines the strengths of Bubblesort and Mergesort.
In order to do this, Bitonic sort sorts part of the lists in the wrong order
(descending instead of ascending) before merging it into the correct order.
The name (bi-tonic) comes from this. To help with this you should make a
helper function in your a3.py called flip that takes a single argument, either> or < and flips it. So, flip( < ) should return > and flip( `
) should return< ` .
Another thing Bitonic sort has to do so that it doesn’t need extra lists is to
recursively merge as well. So you will need two recursive functions: the
recursive bitonic sort function, and the recursive bitonic merge function.
Like in mergesort, the recursive sort function will need to split the list in
half and recursively call itself on both haves. However, you must do this by
keeping track of indices (or indices and lengths), since you can’t split the
list. You can’t use extra lists, since the entire idea of using bitonic sort
is to avoid using extra lists.
For the recursive sort function you should consider the middle (where you
split) to be half way through the indices available. For example, if the
bitonic sort is called (recursively) with the start index 10 and the end index
21, it should split the list into two halves, 10 to 15 and 15 to 21. (Like in
Python, end of all the ranges are exclusive, the highest index is actually
20.)
For the recursive merge function you should consider the middle (where you
split) not half way, but instead with the upper half having a the biggest
power of two number of items while still leaving some for the lower half. For
example, if the bitonic merge is called (recursively) with the start index 10
and the end index 21, it should split the list into two halves, 10 to 13 and
13 to 21. This is because you have 11 items, and the greatest power of two
less than 11 is 8, and so we give the upper half 8 items, and the remaining 3
to the lower half.
However, before splitting and recusively merging, you need to compare and swap
the first three items with the last three items. So in this example, we’d
compare and swap 10 with 18, 11 with 19, and 12 with 20. Then we’d recursively
call our bitonic merge for 10 to 13 and 13 to 21.
To help with this you should make a helper function in your a3.py called
greatest_power_of_two_less_than that takes a single argument, an integer >= 1.
It should return the greatest power of two that’s less than that.
Examples:
greatest_power_of_two_less_than(4) == 2 # 2^1
greatest_power_of_two_less_than(5) == 4 # 2^2
greatest_power_of_two_less_than(100) == 64 # 2^6
greatest_power_of_two_less_than(32) == 16 # 2^4
—|—
Bitonic sort pseudocode:
- a_list is a Python list
- start is the start index >= 0
- end is the end index <= len(a_list) direction is
<or> - Base case: if start to end is only a single index, return
- let middle be middle index between start and end, rounding down
- call bitonic sort recursively from start to middle
- call bitonic sort recursively from middle to end but with direction flipped
- call bitonic merge from the start to end (using the original direction)
Bitonic merge psuedocode: - a_list is a Python list
- start is the start index
>=0 end is the - end index <= len(a_list)
- direction
- Base case: if start to end is only a single index, return
- let distance be the greatest power of two less than the length between start and end
- let middle be end minus distance
- for each index from start and stopping before middle:
- compare and exchange index with index + distance
- the compare (whether or not to exchange) should be done with the current value of direction
- when direction is <, a_list[index] should be exchanged with a_list[index+distance] if a_list[index] is less than a_list[index+distance]
- when direction is >, a_list[index] should be exchanged with a_list[index+distance] if a_list[index] is greater than a_list[index+distance]
- call bitonic merge recursively from start to middle (direction is unchanged)
- call bitonic merge recursively from middle to end (direction is unchanged)
You will probably want to use a third function to start your bitonic sort with
start as 0 and end as len(a_list) and direction as>. - Here’s another reference for how this works
- The wikipedia page also has some nice diagrams
Write a function in a3.py named bitonic that takes a single argument, a list
to sort in ascending order.
Here are some example traces for bitonic and the way it calls recursively. The
indentation indicates how many calls are on the call stack. (The recursion
depth.) Your code does not have to print these, they are just to help you make
sure your algorithm is correct.
Task 3: Fixed Bitonic Sort
Your goal for task 3 is to use the functions you made in task 1 and task 2 to
create a function fixed_bitonic(size) which takes one argument. You should use
your write_py function, but you’re free to make new bitonic functions based on
the ones you made in task 4. That argument will determine the length of the
list that can be sorted. fixed_bitonic(size) should output a file that
contains a function that uses bitonic sort to sort lists of length size. For
examples, fixed_bitonic(2) should create a bitonic2.py that contains the
bitonic2 function that takes a single argument (a list) to be sorted.
Similarly, fixed_bitonic(3) should create a bitonic3.py that contains the
bitonic3 code.
Running and main()
To mark your code, we will run a different Python file in the same folder.
Your python file must be named a3.py or it will not work! You can test your
own code by using the check1.py from the download folder.
Main should be called it using the format:
if name == “main“:
main()
—|—
No other code except CONSTANTS, functions, classes and comments should be
unindented in your program.
Allowed Imports
from importlib import invalidate_caches
from importlib import import_module
from os.path import exists
from os import remove
from random import randrange
—|—
You are allowed to import any code generated by your write_py by using the
load_function/import_module as long as that code doesn’t import anything.
You aren’t allowed to use any other libraries (besides the ones listed here)
whether or not they come included with python.
No other imports are allowed.
Submission
- Submit only your a3.py. Make sure it is named a3.py.
- Late submissions will not be accepted.


